十二个外观一样的铁球，其中一个次品的重量与其他两个不一样，用天平怎样只称三次，把次品找出来？

[ 本帖最后由 maggie爸 于 2006-12-4 20:20 编辑 ].

两次就够了,为什么三次.

.

两次即可，一、拿两个球分别放在天平两边，如果一样第三个球是次品，一次就得出；
二、如果不一样把较重（较轻的也可）的那个留下，较轻的换上第三个球，
1）如果这次两个一样重，则较轻的为次品；
2）如果第三个球较轻，则较重的那个为次品。
3）如果第三个球较重，则题出错了 。.

上面的3位好厉害！.

不好意思，打字错了，总数　是十二个球．.

（1）分成3堆，每堆4个，任选2堆，如分量一样，则第3堆有次品；分量不一样，则轻的1堆有次品
（2）将有次品的一堆4个分成2堆，每堆2个。分量轻的一堆里有次品
（3）将剩下的两个称重，轻的1个为次品

[ 本帖最后由 悦悦MUM 于 2006-12-4 20:49 编辑 ].

引用:

原帖由 zhy9411 于 2006-11-30 07:27 发表
两次即可，一、拿两个球分别放在天平两边，如果一样第三个球是次品，一次就得出；
二、如果不一样把较重（较轻的也可）的那个留下，较轻的换上第三个球，
1）如果这次两个一样重，则较轻的为次品；
2）如果第 ...

你没搞错吧！有12个球了阿！.

引用:

原帖由 悦悦MUM 于 2006-12-4 20:38 发表
（1）分成3堆，每堆4个，任选2堆，如分量一样，则第3堆有次品；分量不一样，则轻的1堆有次品
（2）将有次品的一堆4个分成2堆，每堆2个。分量轻的一堆里有次品
（3）将剩下的两个称重，轻的1个为次品

分量不一样，不能就确定轻的有次品，因为题目并没有告诉你，次品比正品轻还是重，两者都有可能，因此，你的答案好象不对.

A:分成3堆，每堆4个，任选2堆，如份量一样，则第3堆中有次品
把有次品这一堆中的任意一个球放在边上，拿前2堆中的任意3个球（正品）在天平上和第3堆剩余的3个进行比较，会产生2种情况
1、天平持平，则第3堆中放边上的球是次品，拿一个正品球和次品球在天平上秤一下即知次品球是轻了还是重了
2、天平倾斜，与正品球称重比较可以确认次品球是重（轻）球。再将这3球中的2个放上天平，如重量不一致，重（轻）的那个是次品，若持平，没上天平的是次品

B:分成3堆，每堆4个，任选2堆，如份量不一样，则次品在天平上的2堆中
在重的一端取走三个球放在一边，再将剩下的一个球和轻的一端中的一个球做交换，最后从第三堆里补上3个球（正品）后在天平上秤重会有3种情况
i、天平持平了，说明次品在取走的三个球中，而且是重球，接下去用上面A2的方法再上2次天平即可甄别出次品球
ii、天平的倾斜方向不变，那么可以断定，次品是在轻的一端没有作交换的三个球中，而且是一个轻球。同上原理再上2次天平即可甄别出次品球
iii、天平的指针转向了反面，那么，次品球就在做交换的2个球中，用一个好球与其中的一个球上天平秤一次或二次就可以确定哪一个是次品球，知道次品球是轻了还是重了

很多年前解过，再复习一遍

[ 本帖最后由 多多侠妈妈 于 2006-12-5 15:20 编辑 ].

PFPF,很妙的解法！.

过奖了，这样的逻辑题做起来蛮好玩的，不过让小孩子做是难了点.

是好玩的，已经灌给偶家孩子啦，能记得几天就不知道了。.

一个钝角三角形最少可以分为几个锐角三角形？.

至少要7个锐角三角形，才能把一个钝角三角形分解成锐角三角形的组成。.

居然要7个？

为什么不是3个？
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

孩子瞎做，3个肯定错的！楼下那位别汗颜了！

[ 本帖最后由 上海的考拉 于 2006-12-7 00:02 编辑 ].

3个是怎样的？   我也只能拆成7个。  能画一下吗？

-------------------------------------------------------------------------------------------

哦，知道了。暂时不汗颜了。

但不知道7个对不对，如果不对，再汗颜吧。

[ 本帖最后由 springmum 于 2006-12-7 08:17 编辑 ].

答案是七个.

还是一句老话——做题要给思路，否则还当是做题竞赛呢！.

1. 先证7是最少的数目, 并给出一个例子
    如图1,ADEFG是正五边行,O为它的中心,延长AD, FE, AG, EF便得三角形ABC,
    易证其中每个小三角形都是锐角三角形.
    (△AOD, △AOG, △ODE, △OEF, △OFG, △BDE, △CGF)

    以下说明7个是最少。
    ∠A为钝角,必须从A引出一条线,这条线若是到达对边,
    则得到的三角形中又有一个钝角三角,题目回到初始状态，不可。
    这条线若不与对边相交,则必在三角形内终止,设为O点.
    O点处圆周角至少分为5个角才能保证都为锐角,这样便有了5个三角形,
    再加上B,C处两个,至少7个。

20061208-a.JPG (5.61 KB)

2006-12-8 22:22

  
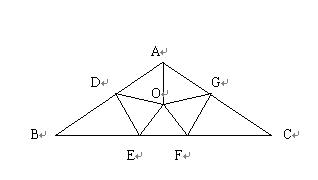
图1
   

2. 再证必然性, 并给出剖分方法
   易知,顶角为锐角的等腰三角形必为锐角三角形[#1].
   如图2
   设A为钝角,作出三角形内心O (角平分线的交点), 则AO,BO,CO都是角平分线。
    作∠BOD = ∠BOE = (∠A+∠C)/4, ∠COF = ∠COG = (∠A+∠B)/4
    则△BDE, △ODE, △CFG, △OFG都是等腰三角形,
   ∠DOE = (∠A+∠C)/2 < 90°, ∠FOG = (∠A+∠B)/2 < 90°,
    据#1, △BDE, △ODE, △CFG, △OFG是锐角三角形.
   ∠OEF = ∠ODA = ∠B/2 + (∠A+∠C)/4
                  < (∠A+∠B+∠C)/2 = 90°
   ∠OFE = ∠AGO = ∠C/2 + (∠A+∠B)/4 < 90°
   ∠DAO = ∠GAO = ∠A/2 < 90°,   
   ∠AOD = 180°- ∠A/2 - (∠B/2 + (∠A+∠C)/4 )
            = 180°- (∠A+∠B+∠C)/2 - (∠A-∠C)/4
            = 90° - (∠A-∠C)/4 < 90°,
    同理
   ∠AOG = 180°- ∠A/2 - (∠C/2 + (∠A+∠B)/4 ) < 90°,  
   ∠EOF = 180° - (∠B/2 + (∠A+∠C)/4 ) - (∠C/2 + (∠A+∠B)/4 )
           = 180° - (∠A+∠B+∠C)/2 - (∠B+∠C)/4
           = 90° - (∠B+∠C)/4 < 90°
    故7个小三角形都是锐角三角形。

20061208-b.JPG (14.68 KB)

2006-12-8 22:32

  
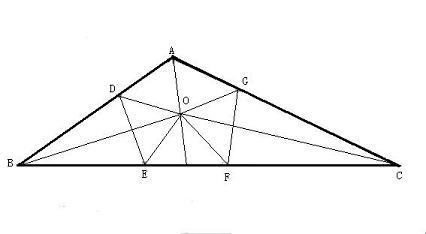
图2

[ 本帖最后由 helenLee 于 2006-12-8 22:32 编辑 ].

LEE,你太厉害了,偶太佩服你了.

.

好MM，领教helenlee多次了！.

不佩服不行..