

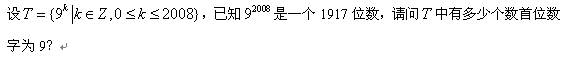
 .
. 
 .
. 
 .
.  终于解出来了。奖励有吗?.
终于解出来了。奖励有吗?. 原帖由 wood 于 2008-1-17 22:17 发表
6楼的题征解继续。
再来征解一个与2008相关的组合题:从1,2,3,。。。,2008中最多能选出多少个数,使得其中任意两个数的差不等于8,也不等于3。要求有完整解答过程。

原帖由 ITmeansit 于 2008-1-18 02:48 发表
我们把这2008个数补一个3^0=1,一共2009个数进行分组,位数相同的数分在一起,根据3^2008是个959位数,当首位数是9的时候,该位数的数字有3个,如1,3,9,而27.81是不会出现9的。我们知道共分为959组,每组要么3个数,要么2个数。设3个数的x组,2个数的y组。
则有x+y=959,3x+2y=2009(补上3^0=1了),解得x=91,也就是说恰好有91组有3个数,该组的第三个首位是9。


 .
. 

 .
. 
 .
. 原帖由 老猫 于 2008-1-18 09:06 发表
哈哈,奖励是我的了。
由于题目中说明3^2008是个首位为1的959位数,所以设3个数的x组,2个数的y组。
则有x+y+1=959,3x+2y+1=2009(补上3^0=1,+1是因为考虑到3^2008是个首位为1的959位数),解得x=92,也就是 ...
 因此这个组里只有2个数。看来我的计算应该是正确的,还请wood验证一下。
因此这个组里只有2个数。看来我的计算应该是正确的,还请wood验证一下。| 欢迎光临 旺旺网 (http://ww123.net/) | Powered by Discuz! 6.0.0 |