

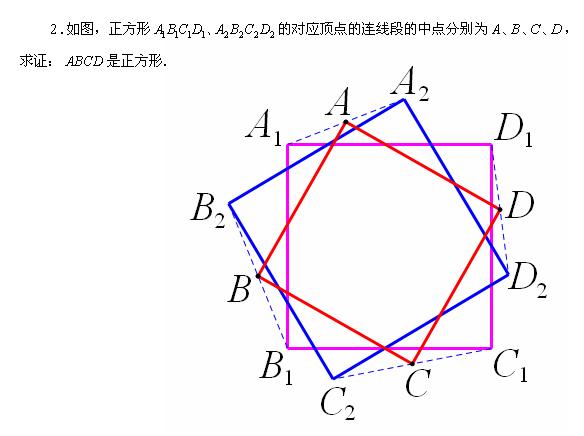

 .
. 
原帖由 后生可畏 于 2008-9-19 08:35 发表
又来啦
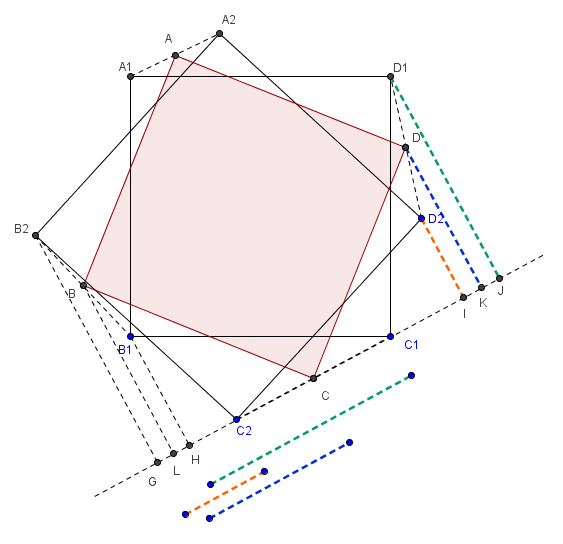
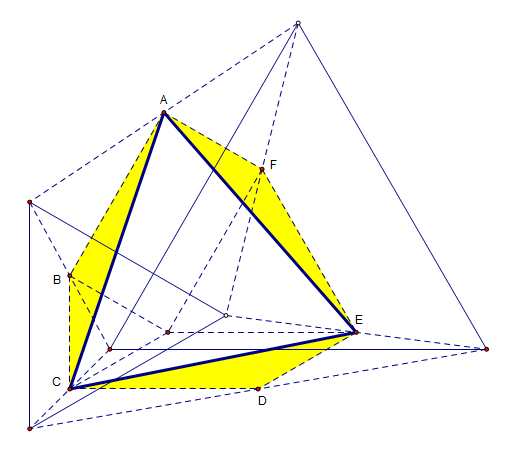
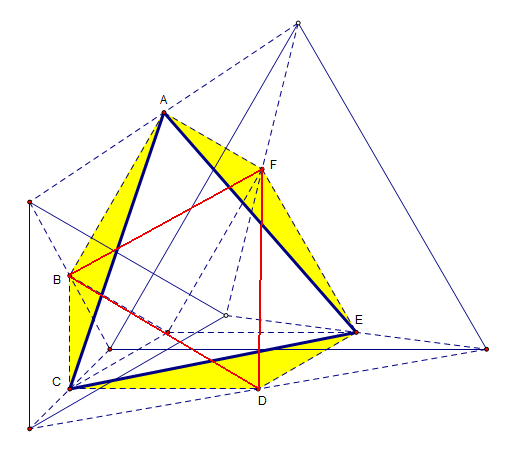
由B、B1、B2、D、D1、D2向C1C2延长线作垂线,
分别交于点L、H、G、K、J、I。
容易证D2I=GC2、D1J=HC1,
而DK=(D1J+D2I)/2(梯形中位线性质),
同时,CL= (GC2+HC1)/2(L和C分别是GH和C1C2的中点,计算 ...
 .
. 
 .
.  .
.  .
. 
 .
. 

 .
.  .
. 
 .
. 




 .
.| 欢迎光临 旺旺网 (http://ww123.net/) | Powered by Discuz! 6.0.0 |