引用:
原帖由 超超他爸 于 2008-12-20 20:17 发表
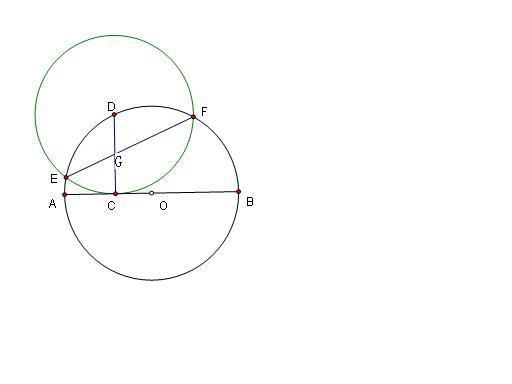
AB是圆O的直径,AB上取任一点C,作AB的垂线,与圆相交于D,以D为圆心,CD为半径,作一圆,与圆O相交于E、F,连接E、F,EF与CD相交于G,求证:G点平分CD。

原帖由 超超他爸 于 2008-12-20 20:17 发表
AB是圆O的直径,AB上取任一点C,作AB的垂线,与圆相交于D,以D为圆心,CD为半径,作一圆,与圆O相交于E、F,连接E、F,EF与CD相交于G,求证:G点平分CD。
原帖由 greenjyz 于 2008-12-21 08:42 发表
也是这么想的,但是有点想糊涂了,请大师看看错在哪?
1\可证EC*CF= OB^2 - OC^2 = DC^2 = DE*DF;
2\三角形DEF的面积 = DE*DF*EF/4/OB; 三角形ECF的面积= EC*CF*EF/4/DC;结果是不等哎?........
糊涂了糊涂了.... ...

 .
. 原帖由 超超他爸 于 2008-12-21 20:58 发表
老姜,我知道了。
延长DC,交上圆于K点,交下圆于H点。
根据相交弦定理,有KG*GC=EG*GF,DG*HG=EG*GF
故:KG*GC=DG*HG
(KD+DG)*GC=DG*(HC+GC)
KD*GC=DG*HC
因为:HC=DC=KD,
所以:GC=D ...
 .
.| 欢迎光临 旺旺网 (http://ww123.net/) | Powered by Discuz! 6.0.0 |