又来啦

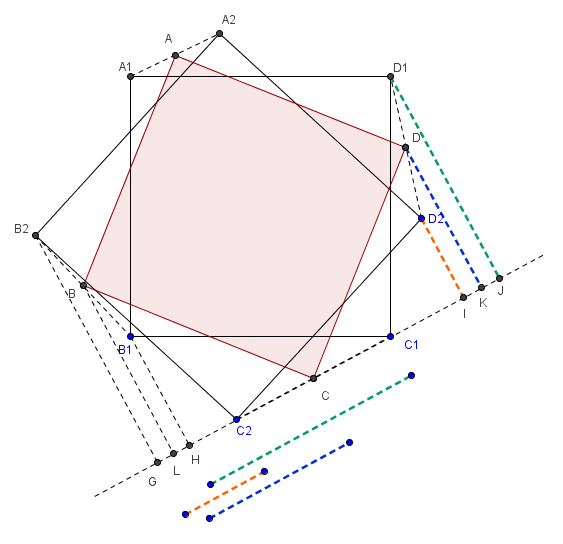
由B、B1、B2、D、D1、D2向C1C2延长线作垂线，
分别交于点L、H、G、K、J、I。
容易证D2I=GC2、D1J=HC1，
而DK=(D1J+D2I)/2（梯形中位线性质），
同时，CL= (GC2+HC1)/2（L和C分别是GH和C1C2的中点，计算可得）。
所以DK=CL，同理BL=CK。可得△BLC≌△CDK。
所以，BC=CD。同理可以证得AB=BC=DA。
角BCL+角CBL=角BCL+角DCK=90度，即角BCD=90度，所以四边形ABCD是正方形。
证毕.

考试考得差不多了，又可以定下心来玩几何了。
姜老师，阿拉继续好伐？呵呵.

主要是我比较空
.

7楼本意是想请您解答一下上面那道三角形“万花筒”的，
想了好几天都没想出来。.

谢谢IT的题示,这题证出来.
证出了3个黄色三角形全等就行了.
具体过程就省略了.

20081122.GIF (13.52 KB)

2008-11-23 20:13

[ 本帖最后由 后生可畏 于 2008-11-23 20:13 编辑 ].

对的，顶点的连接方式不同，可以形成3个正三角形。

20081123.GIF (13.89 KB)

2008-11-24 09:20

.