恶心无聊奥数又来作怪了！
　　要是让偶和儿子来研究，咱就从2人开始。两人报数时，谁先报数，谁倒霉。显然，不是A先报。
　　3人时，情况又如何呢？
　　……
　　这样玩下去，虽然少慢差费，但从易到难，可以玩得孩子不断动脑子，玩得兴致勃勃！
　　试试看！说不定玩到半途，孩子就开窍了。
　　一下子就想找通项式，找出来了，结果又咋样呢？不妨报告一下，交流一下，对比一下：哪一种辅导方案更有利于孩子数学进步？.

　　按照奥巴马的建议，可以这样辅导孩子。（想象的，并没有真正试过）

　　当儿子来请教时，BB不懂不要紧，懂了也要装傻：儿子呀，我也不知道谁先报数，A才能最后幸存。说不定就是A因为最积极第一个报数所以最后幸存下来了。你不如试一试。
　　儿子开始作实验，从A开始报数，经过几个回合的一二三，最后剩下的是H。儿子开始怀疑：老爸，不是A，是H。你怎么出这么个馊主意？
　　儿子啊，你要是让A换到H的位置，最后剩下的不就是A了吗？
　　怎么换啊？
　　这个你别问我，你自己动脑子。
　　儿子便让H先报数，结果最后的幸存者并不A。儿子糊涂了。
　　老爸问：H先报数，最后剩下的是谁呢？
　　O小朋友。
　　A小朋友先报数时最后剩下H小朋友，H先报数时最后剩下的上O小朋友，这里面有什么规律吗？
　　老爸，我知道了，最后剩下的一定是第八个报数的小朋友。
　　要让A小朋友在第八个报数的话，那就要让几位在他之前报数？
　　7个。
　　在这个16人围成的圈子里，是哪7个小朋友？

幸存.PNG (7.01 KB)

2009-3-5 17:31

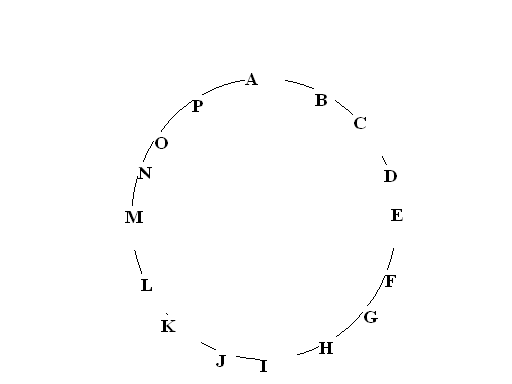
　　JKLMNOP这7位小朋友，应在A小朋友之前报数。
　　所以，要让A最后留下的话，第一个报数的是谁？
　　J小朋友第一个报数时，最后的剩下的会是A小朋友。
　　这只是推理。到底对不对，还要算验证一下。
　　儿子检验了，确认J先报数，最后剩下的是A。
　　BB不能以此满足。要和儿子一起总结经验教训，尤其要让孩子体会到：第一，不要怕难。钻研过后，你会发现并不难。第二，在不知道怎么寻找答案时，可以假定一个答案，然后去验证它；第三，如果假定的答案被证明不对，也不要放弃，可以再作假设再验证；第四，根据错误假设推导出来的结果，往往非常重要，利用它们可能就可以找到正确答案。

[ 本帖最后由 hxy007 于 2009-3-5 20:56 编辑 ].

　　儿子要来问，就算是知道答案，也千万不能直接告诉他。要让他从一道他不会解的题中，学到尽可能多的东西。
　　最好是从最简单游戏的开始：如果游戏中只有两个小朋友ab，谁先报数，a会最后留下呢？
　　傻瓜也能回答：b报“一”，a报“二”，b再报“三”。b出局，a会留下。BB记下：ba
　　如果是3个小朋友abc，要让c先出局a最后留下，那么按什么顺序报数？
　　儿子在abc和bac之间权衡一下，会选择后者的。BB记下：bac。
　　如果又来了个小朋友d，出局的顺序是dcba，那么报数顺序是什么样子？
　　一番探索，结论是：acdb。
　　再加一个小朋友e，出局顺序是edcba，报数的顺序是会是什么样？答案是：dbeac。
　　爸爸在这个时候，应该指导儿子总结排序的规则：先把新来者放在前一轮队伍的排头，再把队伍后两位调到前头（实际就是使原来倒数第二第一报数者改为第一第二个报数的），使新来者报数说“三”从而立即出局。呵呵，这是一个专门欺负新来者的恶心游戏。
　　总结出了这个游戏人数逐渐增加的排序规则，后面的事情就一帆风顺了。
　　b—ba（两人玩时，a第2个报数，将最后幸存）
　　c—bac（3人玩时，a第2个报数，将最后幸存）
　　d—acdb（4人玩时，a第1个报数，将最后幸存）
　　e—dbeac（5人玩时，a第4个报数，将最后幸存）
　　f—acfdbe（6人玩时，a第1个报数，将最后幸存）
　　g—begacfd（7人玩时，a第4个报数，将最后幸存）
　　h—fdhbegac（8人玩时，a第7个报数，将最后幸存）
　　i—acifdhbeg（9人玩时，a第1个报数，将最后幸存）
　　j—egjacifdhb（10人玩时，a第4个报数，将最后幸存）
　　k—hbkegjacifd（11人玩时，a第7个报数，将最后幸存）
　　l—fdlhbkegjaci（12人玩时，a第10个报数，将最后幸存）
　　m—cimfdlhbkegja（13人玩时，a第13个报数，将最后幸存）
　　n—jancimfdlhbkeg（14人玩时，a第2个报数，将最后幸存）
　　o—egojancimfdlhbk（15人玩时，a第5个报数，将最后幸存）
　　p—bkpegojancimfdlh（16人玩时，a第8个报数，将最后幸存）

　　就是说，在16人玩这个“一二三”游戏时，如果开始报数时的顺序是bkpegojancimfdlh，那么，报到“三”出局的依次是ponmlkjihgfedcb，最后剩下的是a。换而言之，无论用什么代号，第八位报数的，一定是最后幸存的。因此，在ABCDEFGHIJKLMNOP这16个小朋友围成一圈进行的游戏当中，要使A最后幸存，第一个报数的必须是J小朋友。

　　在hxy007看来，这算不上是一道“数学”题，尽管它很搞脑子，大人带孩子玩玩也很有趣。但是，作为“数学”考题考小孩子，很不合适！
　　继续玩下去，就会有“数学”味道了！——
　　为了能够解答16人玩“一二三”游戏谁最后幸存的游戏，咱们顺便把2~15人游戏的幸存法则统统摸了个遍。有了这么多数据，如果小朋友还有兴趣玩下去的话，007是可以跟他另做一个游戏的。比如，咱不用像前面那样傻排，就可以断定：
　　17人玩时，A第11个报数，将最后幸存；
　　18人玩时，A第14个报数，将最后幸存；
　　19人玩时，A第17个报数，将最后幸存；
　　20人玩时，A第20个报数，将最后幸存；
　　21人玩时，A第2个报数，将最后幸存；
　　22人玩时，A第5个报数，将最后幸存；
　　……
　　不信的话，试试看！
　　呵呵，好像里面有什么通项式哟。

[ 本帖最后由 hxy007 于 2009-3-6 01:34 编辑 ].

　　上述两个方案都试一下，再比较一下，至少会有两个发现：第一，两个方案花的时间差不多（如果第二方案只玩到找出正确答案的话）；第二，孩子在第二方案比在第一方案更加主动，更动脑筋，从中得到更多的收获。
　　如果第二方案后半部分也顺利实施的话，孩子最终会发现：如果已知若干个（设n个）小朋友的游戏中A在第几位（设x）报数时会最后幸存，则在多一个（n+1个）小朋友的游戏中，A在第x+3位报数时会最后幸存（这好理解，因为每增加一位游戏者时，都把他放在第三位报数，同时把队伍最后两个小朋友调在第一二位，A报数时自然要推后三位）；但是，如果从队伍后面调到队伍前面的两位小朋友中有一位就是A的话（3、4、6、9、14、21人玩时都出现了这种情况），理论上求出的A报数的排位数值就会大于游戏的人数（x+3>n+1），那就表示多数了一圈，A实际的报数排位数值就应当减去一圈人数，即(x+3)-(n+1)，也就是说，A第x+2-n位报数时会最后幸存。这个折算，说起来貌似复杂，实际操作却当简单。
　　如果想让孩子既理解其中的道理，又让孩子在恶心奥数考试中能够快速反应，可以又管齐下。先用第二辅导方案，后第二辅导方案，前详后略，则可面面俱倒了。.

详见http://ww123.net/baby/viewthread.php?tid=4564875&page=34.

引用:

原帖由 helen9401 于 2009-3-9 10:58 发表
好复杂的题目。

　　有人说，还是一年级的题目。上海的小一生好惨啊！.