从一年级暑期开始时,翻看了二年级的数学教科书,发现儿子要开始学习正方形、长方形、面积和乘法了,于是有意识的给儿子引入几何学的基础知识。当时做的时候比较零碎,下面慢慢总结一下,供参考。
注意:以下几何定义,均指平面,除非特别说明。
先转一段大学教授的大实话
三、幾何學生活應用:
日常生活應用:以畢氏定理為例。
畢氏定理:一個直角三角形兩直角邊的平方和等於斜邊的平方。
1.設計建築房屋、設計結構與計算建材都用的到
2.測量距離、高度、深度、寬度。
3.戰爭、狙擊手、砲兵、飛彈射擊。
4.航行計畫圖、飛行計畫圖的製圖。
5.應付學校考試。
其中幾何學對於我們學習歷程上有相當大的影響
正方形和长方形
正方形和长方形的概念可以通过折纸来建立,大量的折纸游戏都是从一个正方形或者长方形开始的。折纸游戏从幼儿园大班就可以开始玩了,到了小学一年级可以提一个更高的要求:
如何把一张不规则的纸,裁出正方形或者长方形?
角度
角度在小学一、二年级没有教,但是BBMM们在刻度尺的时候,同时可以三角板和半圆的量角器。这样当同学们学习直尺上的刻度时,就会关心量角器上的刻度是什么意思。
待一年级学习看钟的时候,就可以引入90、180、360度了。
如果看有关突击队的电影,会听见突击队员叫喊:“11点钟方向有狙击手”,这时可以帮助同学理解,什么是11点钟方向,为什么要这么传递信息。
把左右转的游戏改成度数,也可以使同学们对度数的感觉更进一层。
掌握了角度的基本概念以后,可以解决更多的问题了:
1、如何把一个标准的圆形,用手撕出最大的正方形?
2、BB们带过儿子去洗澡吧?那就不要放过淋浴室的手持淋浴头,正好用来打水仗,可是淋浴头的水怎么才能冲的远呢?
实验证明三角形的内角之和等于180度
1、裁出一个古怪的三角形。不古怪,儿子没兴趣,一说搞怪,劲头就来了。
2、标出三个内角。
3、用剪刀减下三个内角,拼接在一起,“奇怪,怎么正好180度?”
4、再想一个更加古怪的三角形,再试试。
问题:
三角形里边会有2个直角吗?证明之。
长方形的面积
按照维基百科的说法:
面积是对一个平面的表面多少的测量。对立体物体表面多少的测量一般称表面积。
http://zh.wikipedia.org/wiki/面积
这个解释相当抽象,从历史上说,面积的测量是跟土地的私有化密切相关的。中国历史上也曾经发生过几次大的土地测量运行。例如康熙朝,杀鳌拜的理由之一就是侵占皇家土地,到了雍正、乾隆时,如何分配治淮、治黄后新增的土地,也曾经是一个危机到社会的大问题。当然,搞数学的人不自量力讲历史,各位也只能当八卦听听。
其实面积没那么复杂,Alex理解的面积就是数一个图形里边包含有多少个方块,当然这个方块是标准的。
1、用三角板画出某一长宽的长方形,如3厘米X4厘米。
2、画方格。
3、在学九九乘法表之前,只能数方格。
4、学乘法以后,就可以用简单的乘法计算面积。这时,同学们会猜到一个基本公式,长方形的面积 = 长 X 高。可能吧,这是个猜想,如果您觉得验证很重要,那么请验证。
5、做一个有趣的变化,随便裁一个长方形,测量长和宽,再计算面积。因为是随便裁的,所以长或者宽必然带有毫米的“须须头”,我们看看同学们会怎么解决这个“须须头”。
6、回到我们的基本公式,再次验证长方形的面积是否等于长 X 高。
平行四边形的面积

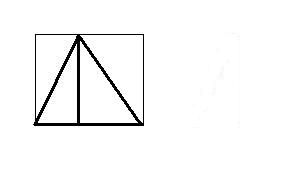
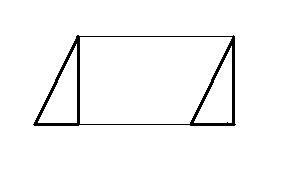 三角形的面积
三角形的面积

 圆的面积是否与周长有关?什么关系?
圆的面积是否与周长有关?什么关系?
未完待续、、、
[
本帖最后由 ccpaging 于 2009-1-13 22:52 编辑 ].