估计名校也在反思。这两天的复旦、交大自主招生面试，考察的是“有社会责任感、道德意识、学习能力、创新精神”、“健康、真实”------至少，这也是种导向吧。.

引用:

原帖由 hxy007 于 2008-11-20 17:00 发表
　　发完上个帖（第149楼）向数学老爹ccpaging请教后，俺就启程出差了。一路之上俺在想，如果数学上不能证明（x+24)/x=1成立的话，那数学就有缺陷，数学就不够完美。

　　儿子1岁时，船长25岁，是儿子的25倍；
　 ...

喜欢这种浪漫，而且还富有哲理。.

昨天才发现这个贴，看了2天才看到18页。
各位大侠饶了我吧，慢点下贴
不然到何时才能赶上进度啊.

某班共有学生38人，其中27人会游泳，23人会骑自行车，30人会打乒乓球。这个班至少有多少个学生三项运动都会？

我们来试试新的解法。

一、数形结合
  这道题从一开始，就要高呼：“儿子，拿笔和纸来。”
  好像数学进入二年级，数学题就不再是那么一针见血了，总是要多多少少地绕上一两个小圈子，所以，仅仅是凭空思考会觉得有些不够，内存小啊，怎么办？
  装“外存”先，准备好纸和笔，随意的记录下思考的内容、过程，从这些记录中寻找最后的结果。
  前面有老数学家讲到数形结合的重要性，比较抽象，可能没有引起足够的重视。后来运用了毕达哥拉斯的数形结合方法，给二年级小朋友解决了根号8和根号2的问题，该次教学实践的成功，印证了数形结合的强大威力。所以，至此以后，我们的数学研究增加了2样必不可少的工具--铅笔和草稿纸。

二、不要只盯住结果，关注问题，循序渐进
  我们先在草稿上画一个圈，这个圈代表了全体同学，38人；
  在全班同学这个大圈里边画第二个圈，游泳的学生，27人；
  画第三个圈，骑自行车，23人，这时我们碰到问题了，骑自行车的和游泳的加起来超过学生总数38人，这里为什么会多出来12个同学？
  如果游泳+自行车等于总数，是什么情况？
  如果游泳+自行车小于总数，又是什么情况？
  经过以上分析，我们可以知道答案，这多出来的12个同学就是又会游泳又会自行车的同学（至少）。

三、化繁为简
  在上图中，我们已经画了3个圈了，一个大圈套了2个交叉的小圈圈，显然，如果要再画第4个圈--打兵乓球的同学，整个图形就有点乱了。
  所以，充分利用二的结果，我们用全体同学38人、又会游泳又会自行车的同学12人、打兵乓球的同学30人，重新画一张新图，这里多出来4个同学。

四、结论
  于是，可以判定这个班至少有4个学生三项运动都会。

[ 本帖最后由 ccpaging 于 2009-2-13 22:24 编辑 ].

化抽象为形象，是个好办法。.

你家007最大的特点就是争强好胜，真是羡慕！而我家的大宝也正如你所说的很有谦让精神，看来我要转变教育思路了。最近大宝迷上了《三国演义》和电视剧《红日》，希望能有所促进吧！.

你太有才了！
用这个法子，顺便也给孩子一点集合方面的启蒙。

[ 本帖最后由 hxy007 于 2009-2-14 17:31 编辑 ].

第一题
父：你们班上现在有多少个同学？
子：有49个同学。
父：放学前，老师说：“今天我们班有30个同学吃过冰淇淋，25个同学吃过酸奶。”
子：多了6个同学，为什么？
父：不知道啊。

第二题
父：爸爸、妈妈和Alex一起出去玩，回家以后，妈妈发现，我们今天有2个人吃过冰淇淋，有2个人吃过酸奶。
子：嗯，多一个人，这个人又吃了冰淇淋，又吃了酸奶。
父：那么？
子：我知道了，班上有6个同学又吃了冰淇淋，又吃了酸奶。

注意：
第二题中，Alex仅仅是提出了一个显而易见的猜想，如我们前面曾经提到的，任何的猜想都需要验证。
hxy007的1260#帖，提出了对这类显而易见的猜想的证明方法--反证法。

[ 本帖最后由 ccpaging 于 2009-2-15 12:34 编辑 ].

ccpaging 的办法灵的！叫小五来学习，居然立刻总结出通项公式：X=A1+A2+A3.....An-PX（n-1）.

引用:

原帖由 ccpaging 于 2009-2-14 19:48 发表
第一题
父：你们班上现在有多少个同学？
子：有49个同学。
父：放学前，老师说：“今天我们班有30个同学吃过冰淇淋，25个同学吃过酸奶。”
子：多了6个同学，为什么？
父：不知道啊。
第二题
父：爸爸、妈妈 ...

精彩！高明！！有了第二题作为梯子，解答第一题就水到渠成，也就给了第1254楼的解决方案一把金钥匙！！！
　　亲子数学，关键不在于BBMM会做孩子做不出的题，而在于想出恰当的法子，让孩子理解题意，通过他自己的思考与探索解决问题；着眼点不在于解决一道道难题找到正确答案，而在于解决问题的探索过程，从中体会数学的思维以及思维的乐趣。

引用:

原帖由 hxy007 于 2009-2-12 11:57 发表
　　某班共有学生38人，其中27人会游泳，23人会骑自行车，30人会打乒乓球。这个班至少有多少个学生三项运动都会？

　　用代数方法解决这个问题不难，中学会学到。用算术的方法，最简单的可能是：
　　不会游泳的：38-27=11（人）
　　不会骑自行车的：38-23=15（人）
　　不会打乒乓球的：38-30=8（人）
　　这个班至少不会一项运动的人数，最多是：11+15+8=34（人）
　　因此，这个班三项运动全会的人数，至少是：38-34=4（人）

　　hxy007也想为自己貎似复杂的解决办法，作点辩解。可是，现在儿子正在犯傻，有更加基础的问题需要解决……
　　折腾到晚上9点，才使犯傻的儿子恢复正常（见第1262楼）。唉，在余数问题上犯傻栽跟斗，已经不是第一回了。不知道，这一回能不能一劳永逸地解决问题。
　　儿子安睡了，007才可以安安稳稳地自娱自乐玩奥数！

　　007觉得，ccpaging提出的解决方案是一个正解，一个巧妙的正解。其难点是，想到“多出的人”是何许人也。有了“冰激淋和酸奶的奥数”打底子，孩子可以比较轻松地突破这个难点。007设想的解决方案，则反其道而行之，从“至少不会一样运动的人数”，去推知“三样运动样样都会的人数”。其难点，就是想到这种思路。一旦想到这种思路，接下来的关键，就是弄清楚“至少不会一样运动的人数”至多有几个。这个问题让中学生解，不难。让小学生解，有很大的难度。007也想借用ccpaging倡导的数形结合的方法以及集合思路，提出一个辅导小学生的方案。

　　（一）情境
　　
　　为了刺激孩子更有兴致思考和讨论这个问题，可对原题稍加扩充和修改。
　　明强小学要开运动会了。学校增设了一个“铁人三项”比赛项目，要求参赛者先后进行游泳、自行车、乒乓等三个项目比赛，三项成绩最优异者为冠军。某班共有同学38人，其中27人会游泳，23人会骑自行车，30人会打乒乓球。试问：这个班至少可以从几位同学中选派参赛选手？
　　个人觉得，这种修正可以使孩子们更加理解题意，也更加理解探讨这种数学课题可能的现实意义。

　　（二）问题

　　这个班应该选什么样的同学代表班级参加“铁人三项”比赛呀？
　　选既会游泳又会骑自行车还会打乒乓的同学参赛。
　　用什么办法才能知道这个班有多少同学这三项运动都会呢？
　　请三项都会的同学举一下手。（我cao，竟然这么简单！看来，这个题目是在瞎编！）
　　假定我们不去问那个班的同学，就靠现在的已知条件，我们能够算出这个班至少有几个同学三项运动都会吗？

　　（三）假设
　　
　　好像不能！因为，现在我们只知道这个班有27人会游泳，23人会骑自行车，30人会打乒乓球。可是，我们不知有多少人会两样，更不知道有多少三样都会？
　　别那么快就下结论嘛！让我们一起开动脑筋，想一想。要是我告诉你这和班有18个女生，你们知道这个班有多少个男生吗？
　　知道。38-18=20，这个班有20个男生。
　　对头。你们能不能用相似的办法，算出这班有多少同学三样运动都会呢？
　　要是我们能够知道这个班有多少同学至少有一样不会的话，用38减掉这个人数，就可以算出三样都会的同学有多少。
　　
　　（四）探究

　　你们提出一个很有意思解决方案。现在，我们就试一试。先来看一看，这个班有多少同学“铁人三项”中至少有一样不会？
　　这个班不会游泳的同学有38-27=11（人），不会骑自行车的同学有38-23=15（人），不会打乒乓球的同学有38-30=8（人），加起来，不会一项运动的有11+15+8=34（人）。
　　这样算对吗？这个班要是有一些同学有两样不会，还有一些同学有三样不会，你们这样算不就多算了吗？
　　对的。这就看这个班运气好不好了。运气好的话，不会这三项运动的都集中少数同学身上，三样都会的人数就多；运气不好的话，就有许多同学会两样却不会一样，三样都会的就很少。
　　好吧。运气最好时至多有多少同学至少不会一样运动？运气最差时至少有多少同学至少不会一样运动？你们不要猜。我这里有一些圆圈，我们用它们来做一个游戏。这个最大的黄色圆圏代表这个班有38个同学；第二大的是一个绿圆，代表15名不会骑自行车的同学；稍小的是一个蓝圆，代表不会11名不会游泳的同学；最小是个粉红色的圆，代表8名不会打打乒乓球的同学。请你们摆一摆，运气好是什么样子？运气差又是什么样子？
　　探究出来的理想结果如下图所示：

数.png (26.58 KB)

2009-2-15 01:45

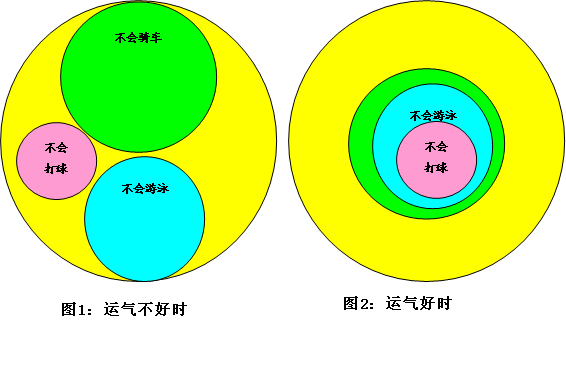
　　运气不好时如图1，绿红蓝三圆不交叉。就是说，这三个圆代表的同学不会某一样运动，但会其它两样，他们都不能代表班级参加“铁人三项”比赛。运气好时如图2，绿圆含蓝圆，蓝圆含红圆。就是说，不打乒乓的同学肯定不会游泳，不会游泳的同学肯定不会骑自行车，因此只要不会骑车就不能代表班级参加“铁人三项”比赛。因此
　　15 ≤ 至少不会一项运动的同学数 ≤ 34（即至少15人，至多34人）

　　（五）结论

　　除去绿蓝红部分，剩下的黄色部分代表的就是三项运动样样都会的同学。根据“三项运动样样都会的人数”=38-“三项运动至少不会一样的人数”，可得
　　23 ≥ 三项运动样样都会的人数 ≥ 4
　　也就是说，这个班至多有23个同学，至少有4个同学，兼会骑自行车、游泳、打乒乓球这三项运动，可以从中派选代表参加“铁人三项”比赛。
　　这道题的解决思路，简单地说就是:

　　“三项运动样样都会的人数”（至少）
　　=全班人数-“三项运动至少不会一样的人数”（至多）
　　=38-（不会骑车的人数+不会游泳的人数+不会打球的人数）
　　=38-[（38-23）+（28-27）+（28-30）]
　　=38-（15+11+8）
　　=38-34
　　=4（人）

　　尽管我们想尽办法试图降低这道题的难度，但是个人认为让小学生做这种题并不恰当。这种题目电流量大太，会烧坏小学生娇嫩的脑子。玩当然可以，只是别当真。当真的话，只对探究过程当真，别在意能否找到答案。就是说，孩子做不出来，或者在有辅导的情况依然不理解，思维跟不上，不要抓狂，不要责怪孩子，不要对孩子的数学能力产生怀疑。相信他，到了中学，解决这种问题小菜一碟！

[ 本帖最后由 hxy007 于 2009-2-16 08:55 编辑 ].

原题
Isabel妈 求助：五年级奥数题
某人要从第一阶楼梯走到第十阶楼梯，他共有三种走法：一次一阶，一次二阶，一次三阶，则他走完这十阶楼梯共有多少种不同走法？
答案是274种

http://ww123.net/baby/viewthread.php?tid=4614542

何为“走一阶，走二阶，走三阶”？
假设有三个人上楼梯：
1、小妹妹，她的人小步子小，一次只能上一个台阶，于是10级抬价要跨10步。
2、小五生，步子大点了，一步可以上二个台阶，于是10级台阶只要跨5步。
3、爸爸看大家在楼道上玩的热闹，耐不住了，也走了一次。爸爸高大多了，一步可以上三个台阶，三步就上了9级台阶。可是笨爸爸在第9级台阶停住了，因为只剩下一级了，他想了想，只好一脸苦相地像小妹妹那样，上了第10级台阶。

大家跑了这么多次楼梯，都有点累了，一起拥进了家里喝水。小五生拿起了铅笔和草稿纸，又开始写写画画了，画的什么呢？请小五生讲给我们听吧。

（小五生要开始讲课了，大家快找沙发坐下、、、）

笨爸爸的脚上有鸡眼
前回讲到小五生若有所思地在草稿上写写画画，在大家喝水的当口，宣布了他的发现：

笨爸爸如果聪明一点的话，就可以发现，他其实有很多种走法，例如：
1+3+3+3，第一步走一级，再分成三步，每步三级。
3+1+3+3，第一步走了三级，有点气喘，第二步走了一级，后面三级一步。
、、、、

大家听了以后都一脸茫然，小妹妹问：”小五哥哥，你在说什么啊？“
为了使大家都明白是怎么回事，小五翻出了妹妹的玩具，有些是红色的方块，比较窄，有些是黑色的方块，长度正好红色方块的三倍，如图摆放。

第一次爸爸走的样子
+----+ +----+ +----+ +-+
第二次爸爸走的样子
+-+ +----+ +----+ +----+
第三次爸爸走的样子
+----+ +-+ +----+ +----+
第四次爸爸走的样子
+----+ +----+ +-+  +----+

小五生总结道：”爸爸有四种走法。“
笨爸爸终于明白过来了，可是爸爸不服气，对小五说到：
”如果在平时，这点步法也算不了什么，我的凌波微步功还没用上呢！但是，今天我脚上鸡眼有一DD痛，也可能一步走二级哦。“
小五当场晕倒：”我怎么把鸡眼给忘了啊？事情有点复杂了，大家请继续喝水，我研究去也。“

领悟
第一眼看到这题，感觉可能性蛮多了，但是没想到有274种之多。
目前为止，我们还是深一脚浅一脚的在黑暗中摸索，不过，这也比开始茫然不知所措好多了。这是黎明前的黑暗，最黑的一段时间，却已经孕育了希望。
在小五发现笨爸爸的鸡眼发作时，也同时领悟到这道题就是不同步幅之间的排列组合，很像一二年级做的数三角形、长方形的题目。

都是鸡眼惹的祸

小五生回到了自己房间开始回想刚才的情景，本来以为已经得到答案了，却被笨爸爸的鸡眼困住了。多么令人讨厌的鸡眼啊！

于是，小五生定下心来，决定从小妹妹开始研究。小妹妹的情况是最简单的，只有一种情况，那就是一步一步地走上来。
1

研究到小五生的情况就有一点复杂了，小五可以一步一级，也可以一步二级，例如：
1、可以走1步二级的，余下的一步一级；
2、上面1的情况，还可以随意插在任何位置；
3、也可以走2步二级的，余下的一步一级;

看起来，我们开始的时候必须分情况计算了。
1、只走一次二级步的
+--+ +-+ +-+ +-+ +-+ +-+ +-+ +-+ +-+
这种情况下，一共有9种走法

2、走二次二级步
、、、

小五生开始困惑了，这要走到什么时候啊？

最佳答案
小五生回忆到设计数三角形和长方形的通项公式的情景，突然灵光一现，似乎可以用递增楼梯级数的方式去研究。也就是第一次考察有一级楼梯的情况，以后依次递增，比较每次增加楼梯级数后产生的增量。
想到这小五生似乎看到了曙光，在书房里奋笔疾书地开始计算起来。不过小五生忽略了一件事情，那就是笨爸爸还在楼梯间爬上爬下地计算走法呢！
小五生终于得到了一下结果。

摘自：http://zhidao.baidu.com/question ... r=qrl&fr2=query
从只有一级时级开始考虑.
共一级时1种,共二级时2种, 共有三级时第一步若迈一级, 则剩下二级, 迈二级, 则剩下一级, 迈三步则正好. 所以共有2+1+ 1= 4种.
按这种方法得到递推公式
S4=S3 + S2 + S1
所以S10=274种.
好多啊, 幸亏没挨个数.

笨爸爸在楼梯间喊道：“儿子，我都爬了N次楼梯了，你有没计算出来啊！”
小五生忙道：“不用爬啦，我已经发现错误了。”
笨爸爸气喘吁吁地回到屋里，一边那毛巾擦汗一边责怪小五生：“儿子，那是爬楼梯啊！你这一错不打紧，我白爬了多少楼梯啊。”
小五生噘嘴辩解到：”我是错了，但是”错误“的结果是帮你减肥，这叫'负负得正'。你说过的，减肥茶就是质量不好的茶叶，一个道理，蒿？！“
============================
另有chenhao920的正宗解法，详见
http://ww123.net/baby/viewthread.php?tid=4614542

ccpaging这个笨爸爸同学目前爬楼梯减肥中、、、!

[ 本帖最后由 ccpaging 于 2009-2-15 15:28 编辑 ].

　　儿子遇到了一个令人不安的问题。问题不在不会做某道题，而在早先学过的一些数学连最基本的东西都没有过关。
　　这次周未卷有一道题：有3叠本子，每叠42本，平均分给5个小朋友，至少再添加几本才正好分？
　　儿子苦着脸来找hxy007，他说：不管怎么添，都没办法做到正好分完？
　　怪哉！007赶紧让他说说，他是怎么分的。儿子立即拿出他打过的草稿，被制止。007要他当面算一算，讲一讲：到底怎么个分不完？
　　儿子说：5个小朋友要分的本子总共有42*3=126（本），126/5=25……1（本）；要是添加1本，就是127本，127/5=25……2（本）；要是添加2本，就是128本，128/5=25……3（本）。你看，不管加多少本，总是会多出几本来。
　　我晕，到小三第二学期了，还会有这种高论！看来，当年儿子学除法和余数，学得不扎实。或者说，当年老师教除法和余数，教得太快，并没有让学生真正理解、领会除法及余数的概念。这一课得赶紧补上！
　　007顺着儿子的思路开始装傻表演：是耶！——129/5=25……4（本）; 130/5=25……5（本）；131/5=25……6（本）。看来，你说得对，好像是不管126加多少都没有办法让5除完。
　　儿子满脸狐疑，看着老爸边说边写。当007说到余数是6时，他再也忍不住了：这个余数不可能是6！他用竖式演算出131除以5得26余1，试图以此说服他老爸。
　　007不买帐，也用竖式演算：131除以5，得25余6。
　　看着007的演算过程和结果，小三生气坏了，憋了好一会儿，终于说出了反驳的理由：老师说了，余数不能和除数一样大，更不能比除数大。
　　反问：余数为什么不能和除数一样大？余数要是和除数一样大，那就表示什么？
　　答曰：余数和除数一样大，就表示被除数可以除尽，商要再加1。
　　又问：我们试着做了这个题，哪个数可以被5除尽啊？
　　子曰：130.我知道了，这个题目的答案是4！
　　父：你是怎么样算出来的？
　　子：先给126加1，看看能不能被5整除。不能整除的话，就加2，再看能不能被5整除……试到130，130能被5整除。所以130-126=4（本），要再添加4本才能正好平分。
　　父：这个题目真烦人，是不是？有没有更好的办法？
　　儿子露出一副困顿不解的样子。007看着，快要崩溃了，压住火气问：126不能被5整除，是不是？
　　是。
　　余数是多少？
　　1。
　　能不能让126变成一个别的数，好让它能被5整除？
　　能。这个数是130，126变成130就能被5整除。
　　我还有其它答案，126变成135、140、145……都能够被5整除。也就是说，126加4、9、14、19……都可以被5整除，所以你的答案好像不对哟！
　　儿子这会儿脑子转过来了：题目是问“至少再添加几本才正好分？”所以答案应该是4，不是比5大的答案。
　　007不依不饶：你为什么提到5？为什么答案一定要比5小？
　　子答：余数1加上4，就够被5来整除了。
　　007加了一把火：那么，你这答案除了可以用130-126算出来，还可以什么办法算出来？
　　子恍然大悟：5-1=4.
　　什么意思？
　　除数减去余数，这个得数加到被除数里，它们的和就可以被整除。
　　007肯定了这个总结，但意犹未尽：刚才说，让126变得再大一些，说不定就可以被5整除。现在来看一看，126不变大，能不能被5整除？
　　子曰：不变大，就变小。126变小一些，也有可能被5整除。
　　比如说，变多小？
　　126减去1，得125，可以被5整除。
　　还有呢？
　　120也可以被整除。对了，我想起来了——只要个位数是0，或者是5，这样的数都能被5整除。

　　LP旁听了许久，火冒三丈，忍无可忍，把父子俩狠狠地教训了一番：这是一个故事！说的是5个小朋友分126本本子，平均分下来，多出了1本。现在要你们想个办法，让他们每个人分得一样多。
　　007立即响应：对对对，这个问题很简单。要是让我来分，我就把多出的那1本藏起来，让他们分125本，不就正好可以平分了吗？我要是很自私，还可以藏6本，藏11本……让他们平分得更少。
　　儿子好像也豁然开朗：现在多了1本，要是让我分，我就再多给小朋友4本，加起来是5本，5个小朋友每人又可以多平分1本。要是还有更多的本子，我就会加9本、14本、19本、24本……小朋友们就会平分到更多的本子。

　　对于孩子来说，除法的概念和运算规则以及余数概念，如果脱离了生活，就会变成一些十分抽象而毫无意义的东西。如果要使孩子获得其意义，就要不断地联系现实的生活，去使用这些概念和规则。这是LP大人给007的教训。

[ 本帖最后由 hxy007 于 2009-3-13 17:52 编辑 ].

个人以为这就是属于”三基“的内容，要反反复复地搞，会越来越清晰，越来越扎实。

学好”三基“，中学、大学会走的很顺，”道路越走越开阔“（宋祖英的配唱）。

另外，如学过点、线、面、体以后，有几个必须要问的问题：
点的长度是多少？线的粗细是多少？平面的体积是多少？

[ 本帖最后由 ccpaging 于 2009-2-14 23:19 编辑 ].

引用:

原帖由 hxy007 于 2009-2-14 22:31 发表
　　儿子遇到了一个令人不安的问题。问题不在不会做某道题，而在早先学过的一些数学连最基本的东西都没有过关。
　　这次周未卷有一道题：有3叠本子，每叠42本，平均分给5个小朋友，至少再添加几本才正好分？
　　 ...

这题我家倒是一下子就出来了，可是后面那道汽车运输的题目让我看的冒火，虽然答案是对的，可是明明可以一步到位的题，硬是排了三个式子！害的船长老爹使出杀手钳用汉堡包来举例，小家伙眼一抬立马就得出了答案，问他解题过程，他好是得意，还被他嘲笑了一番。 看来汉堡包的刺激力够强.

我儿子在美国学校里参加了奥数班。  三年级下学期所有三年级学生参加一个智商考试， 通过的学生四年级开始在课余可以参加优才班活动（英文叫GATE (gifted and talented) Program). 他们今年的优才班活动是做奥数题。 每星期一， 星期二下午2：20 到3：00.  

我也去旁听了几节课。  每节课老师会发一张卷子， 每张卷子上有五道题。 每道题要在规定时间内完成。他们一道一道题做。  就比如， 老师说现在大家一起做第二道题， 四分钟后停止， 老师请会做的学生上来讲解。 等他讲完， 老师问：“有跟他不同的解题方法吗？” 所用解法不同的学生一个个上去讲一下。  然后做下一道题。  如果没有人会做， 老师会提示一下， 提示到大家会做了， 然后就像上边的程序一样， 学生做， 学生上台讲。  老师一点也不赶时间， 能讲完几道就讲几道。

每个月会有一次考试， 全国参加奥数活动的小朋友考同样的卷子。 但不会评名次， 小朋友只知道每道题各有百分之几的人做对了。

这是他们上星期做的几道题：

1. （4分钟） 在50和60之间的所有质数的和是多少？

2. （4 分钟） 小明把一个自然数除以2， 把所得到的商减6， 给得到的差开平方。  在平方根上加1. 把和再开平方。 最后得到3.  问小明最初的数是多少？

3. （6分钟） 在一条线段ABCDE上， D是AE的中点， BD的长度是AB长度的2/3. BC=CD. 问： AC是AE的百分之几？

4. （7分钟） 把两个小于20的连续自然数相乘， 再在积上加17.  你会发现有且只有两组自然数经过运算后结果不是质数。  找出这两组数。

5. （5 分钟） 一个电子表上的时间表达方式为： HH:MM. 在一天的7:59am和2：59pm之间有多少分钟HH比MM大？

[ 本帖最后由 小鹿 于 2009-2-15 13:50 编辑 ].

这个方法不错，很像设想的“我不知道”数学社。尤其喜欢不赶时间的氛围。似乎也解决了一个悬而未决的顾虑，如果台下坐了一窝像我这样的笨爸爸和装傻充愣的聪明妈妈，孩子们也能通过孩子们之间的互动变得越来越聪明。

子曰：”三人行，必有我师焉。择其善者而从之，其不善者而改之。"

似乎以孔老师的想法，善者为师，不善者亦可为鉴，为师者不一定是“达者”。

[ 本帖最后由 ccpaging 于 2009-2-15 17:33 编辑 ].

引用:

原帖由 ccpaging 于 2009-2-14 21:45 发表
爬楼梯减肥之五年级奥数题
某人要从第一阶楼梯走到第十阶楼梯，他共有三种走法：一次一阶，一次二阶，一次三阶，则他走完这十阶楼梯共有多少种不同走法？
答案是274种。问：如何解？

　　前面刚刚说过，那道“铁人三项赛”题电量过大，会烧坏小学生的脑子。这道“爬楼梯减肥”题就更不像话，因为它的电量更大，更有可能要烧坏小学生的脑子。好在ccpaging把它变成了一场妙趣横生的数学搞笑游戏，不但降低了此题的难度，增加了趣味性，也提供了一种可行的思路，推动着孩子从尝试-错误中，逐渐探索，寻找到答案。相信老师们也有这种智慧，就是不知道有几个老师有这份胆识和耐心——用几节课的时间解决一个问题，是不是效率太低了？！
　　可是，这样的耐心，引导孩子慢慢地探索，收益是巨大的。想想看，经历过这种探索的孩子，对数学会有什么感受？除了成功地解决一道难题，更重要的是，他对自己的数学能力充满自信，他得到了一次生动活泼的排列组合启蒙教育，不但受到严谨而灵活的数学思维方法的训练，也对数学充满好感——他一定会爱死迷死数学的。这样慢慢来，很值得哟！
　　受此题及ccpaging搞笑方案的触动，先前那道“揪坏蛋”的变态小奥又勾起了hxy007兴趣。儿子不提，难道老子就不去思考了吗？不是说爸爸是儿子身后的那朵浪花吗？得作好准备，说不定哪一天儿子就会旧题重提。

　　（九）“三分重组法”辅导方案：爸爸的设计

　　第1134楼曾经提到：

引用:

原帖由 hxy007 于 2009-2-4 16:39 发表
　　前面的试验性探讨显示，二分法、三分法、四分法都包含了4种可能，其中3种可能，秤3次就可以锁定目标并识别其轻重；唯六分法出现了6种可能，其中3种需秤3次，另外3种需秤4次。比较而言，六分法似乎最不合理。有趣的是，儿子恰恰是在使用六分法进行探索时，出现了前面未曾有过的尝试——为了找到解决办法，他试图在车马炮兵仕相等6组之中寻求不同的组合，这等于是在三分法中寻求跨组的组合。
　　儿子甚至想把双炮、双兵、双仕、双相分别拆开来重组。为了方便和明显起见，007建议他撤下一半的红棋，再补充黑棋车马炮卒士象各一个，跟留下的红棋车马炮兵仕相等6子配起来。这种搭配，更加明显地提示了各种可能的重组，把儿子看得头昏眼花，不知所措。
　　太复杂了！儿子把握不住，放弃了，对007嚷道：老爸，我头晕！
　　那就算了。小小年纪能够想到不断重组这一层，已经难能可贵。足矣！

　　儿子当时放弃进一步思考，除了问题本身过于复杂之外，还与探索的工具不适当有关。黑棋车马炮卒士象和红棋车马炮兵仕相混在一起，确实会令人眼花瞭乱，搞乱思路。看来，探索所使用的工具是非常重要的。适当的工具，可以起到提示方法和降低探索难度等作用。为孩子挑选适当的探索工具，也是亲子数学的题中之意。儿子在探索“揪坏蛋”的方案时已经用过了四色飞行棋、国际象棋、中国象棋，这一回得让他使用陆战棋了。
　　为了让题目与探索工具统一起来，007把JJ出的那道题改编了一下：

　　某陆战棋生产厂家的质量检查员向总经理J夫人报告，最近生产的陆战棋可能存在质量问题。因为他发现“司令”、“军长”、“师长”、“旅长”、“团长”、“营长”、“连长”、“排长”、“工兵”、“炸弹”、“地雷”、“军旗”这12种棋子中，11种重量一样，但有一种棋子跟其它棋子的重量有比较明显的差别。J夫人立即找来技术员，要求他用天平秤12个不同的棋子，只准秤3次，但必须找到那个重量不一样的棋子，并且查明它是比其它棋子重还是比其它棋子轻。假如你就是那个技术员，你会怎么秤呢？

　　先让007当一回技术员吧。007从儿子打乱棋子重新编组的尝试中受到某种启发，琢磨着怎么通过不断重组的方法，秤三次就揪出那个坏蛋，而且知道它的轻重。12个棋子，每次秤8个，这种组合太多，情况太复杂，007把握不住，无数次的尝试都失败了。007只好改弦更张，另谋出路。ccpaging这个“爬楼梯减肥”的故事，还真地启发了007。秤三次保证揪出坏蛋，仿佛又出现了希望的曙光！
　　不但用三分法秤12个棋子存在许多种组合，三次秤下来的结果也会存在多种排列。因为每一次秤的结果只有3种可能的结果，要么天平保持平衡，要么天平左倾，要么天平右倾，因此三次秤下来有3*3*3=27种结果，即平平平、平平左、平平右、平左平、平左左、平左右、平右平、平右左、平右右，左平平、左平左、左平右、左左平、左左左、左左右、左右平、左右左、左右右，右平平、右平左、右平右、右左平、右左左、右左右、右右平、右右左、右右右。
　　可是，在007设想的秤量方案中，那12个棋子个个都要至少过1次秤，潜藏于其中的坏蛋自然不可能幸免，因此不可能出现三次秤量的结果都是天平保持平衡这种情况，接下来就不必考虑“平平平”这种可能的结果了。其余的26种可能，可以组合成13对相反的结果，即平平左-平平右、平左平-平右平、平左左-平右右、平左右-平右左、左平平-右平平、左平左-右平右、左平右-右平左、左左平-右右平、左左左-右右右、左左右-右右左、左右平-右左平、左右左-右左右、左右右-右左左。007在想，要是从这13对结果中选出12对，与12个棋子匹配，似乎就可以变成揪坏蛋并识别其轻重的识别码。
　　选哪12对呢？随便选，应该都可以吧。但007怕麻烦，考虑到已经排除了“平平平”，凭着直觉感到其它含“平”的结果都应该保留。那就只能从那4对不含“平”的结果中排除1对了，排除谁呢？随便排除谁，肯定都可以。可是，007深受古典数学思想的影响，极其崇拜数学中的对称结构。既然已经排除了“平平平”，凭着对称美的直觉，决定让“左左左-右右右”出局。剩下的12对可能的结果，便构成了007揪坏蛋的识别标准。
　　原以为有了识别标准，设计出秤量方案应该一帆风顺了。孰科一尝试，立马撞到南墙上。看来，还有一些东西需要考虑。这12对识别码，007用左半边来界定坏蛋“较重”，右半边用以界定坏蛋“较轻”。可是，照着前面的组合去设计秤量方案，就会出现一次秤量左右两边的秤盘上棋子个数不等这种咄咄怪事！
　　初次设计失败的教训是：第一，这12对识别码左右两半中所含的可能结果加起来，应该各有12次“平”、12次“左”、12次“右”；第二，就左半边的识别码而言，第一次、第一次、第三次秤量所含的可能结果加起来，应该各有4次“平”、4次“左”、4次“右”（左半边做到了，右半边自然随之做到）。惭愧啊，007的矩阵没有学好，或者说学过的矩阵知识都还给了老师，只好用手工调整部分识别码的左右位置，以达到上述两点要求。这种原始办法，弄得007顾此失彼，焦头烂额，费了老大的劲，才弄出一个结果来。
　　下面就是修正过的揪坏蛋识别标准：

　　司令重（轻）：平平左（平平右）——若第一次秤为平，第二次秤为平，第三次秤为左倾，则司令较重；反之，若平平右则司令较轻。下同。
　　军长重（轻）：平左平（平右平）
　　师长重（轻）：平右右（平左左）
　　旅长重（轻）：平左右（平右左）
　　团长重（轻）：左平左（右平右）
　　营长重（轻）：左左平（右右平）
　　连长重（轻）：左右平（右左平）
　　排长重（轻）：左右右（右左左）
　　工兵重（轻）：右平平（左平平）
　　地雷重（轻）：右平左（左平右）
　　军旗重（轻）：右右左（左左右）
　　炸弹重（轻）：右左右（左右左）
　　
　　有了系统的识别标准，接下来就是按此标准设计秤量方案了。第一次、第二次、第三次秤时，左秤盘应该放哪几个棋子，右秤盘应该放哪几个棋子呢？007的脑子有点乱了，这个秤量方案就请J姐或她家小五代劳来设计吧！007等着用这个方案和小三生共同探讨呢。

未完待续……

[ 本帖最后由 hxy007 于 2009-2-17 00:19 编辑 ].

小五下午考完小机灵，现在连脑筋都不愿意动
我倒是感兴趣上面那些美国奥数题呢，小五他爹那种奥数弱智的人都说这些题目好，有根有据，不像我们那些减肥题登山题不着边际。可是，两个笨蛋男人对第4题苦思冥想半天做不出来，还是我，聪明，半分钟解决问题，答案是16、17和17、18，因为，（16X17+17）/17=17，（17X18+17）/17=18，只有它们不是质数，了不起吧，美国小四毕业咯！.

真有意思，美国人出题目也用”小明“。

这种以孩子为主体，也不排名次的做法好，没有那么功利。题目也适合孩子的水平。.

引用:

原帖由 火车是运茶的 于 2009-2-15 21:30 发表
真有意思，美国人出题目也用”小明“。

原题里不是小明， 这不是我翻译了一下吗。

原题里叫Adnan.  (做题的时候小朋友可以直接称呼他为A.  题目里有几个人的话一般命名他们为： Amy (or Albert), Betty (or Brett), Cindy (or Cate), ....  )

[ 本帖最后由 小鹿 于 2009-2-15 21:53 编辑 ].

发重复了

[ 本帖最后由 小鹿 于 2009-2-15 21:54 编辑 ].

不好意思，没怎么看明白。

前面不是已经解决了第一次出现持平的情况了吗？这次完全可以减小点问题的规模啊。.

他们起名字方便，A啊B啊的，一会儿就有方程的雏形了。我们是小明、小……我怎么就知道小明的？.

引用:

原帖由 Jupiter 于 2009-2-15 20:44 发表
答案是16、17和17、18，因为，（16X17+17）/17=17，（17X18+17）/17=18，只有它们不是质数，了不起吧，美国小四毕业咯！

完全正确！  我们可是从1x2开始一项项检查才得到这个结果的！得到结果了才恍然大悟因为 16x17是17的倍数， 再加17仍然是17的倍数， 所以结果就不是质数。

后来小朋友说17这么神奇啊！  那20以内还有没有别的数也是这样的呢？  大家算了一下， 19不行（1x2+19不是质数）， 13也不行（3x4+13不是质数）。 11好像可以， 但没来得及检查到最后几组。

[ 本帖最后由 小鹿 于 2009-2-15 22:09 编辑 ].

从1x2开始一项项检查，7分钟时间不够呢。奥数有别于数学的地方就是有时候不能死算，要找规律。.

那不是第一次做这种题吗 ， 下一次再碰到这种题几秒钟就解决了。

而且我觉得一开始只有这样小朋友才能彻彻底底地明白这类题目。.

引用:

原帖由 火车是运茶的 于 2009-2-15 21:55 发表
不好意思，没怎么看明白。
前面不是已经解决了第一次出现持平的情况了吗？这次完全可以减小点问题的规模啊。

　　这次采取的思路是，第一次一个也不搞定，第二次也搞不定，到第三次全搞定。我已经提出了识别标准，也提出了秤量方案的设计原则，就差具体的秤量方案了。J姐也在网上，不知是否有兴趣一起来讨论。

[ 本帖最后由 hxy007 于 2009-2-15 23:23 编辑 ].

你们那里白人孩子表现如何，是不是华人更聪明？.

引用:

原帖由 小鹿 于 2009-2-15 22:08 发表
那不是第一次做这种题吗 ， 下一次再碰到这种题几秒钟就解决了。
而且我觉得一开始只有这样小朋友才能彻彻底底地明白这类题目。

[  启蒙不要快，快了会似懂非懂，而且容易挫伤探究的积极性。还是慢慢来，比较合乎认识规律。.

我正在阅读你的方案。.

倒也不一定华人小孩更聪明， 但华人小孩（其实应该说亚洲小孩）在父母的管理下更用功， 更忙碌一点。 于是考试成绩要好一点。

[ 本帖最后由 小鹿 于 2009-2-15 22:20 编辑 ].

我怎么觉得你这套思路有问题，你好像想找出通项公式呢，难怪头大。.

引用:

原帖由 Jupiter 于 2009-2-15 22:37 发表
我怎么觉得你这套思路有问题，你好像想找出通项公式呢，难怪头大。

　　依稀记得中学时玩过类似的题目，但需要排查的可疑分子没有这么多。具体怎么弄记不清了，我现在也是在边写边想，有点眉目了，但还没有经过检验。要不，再等一会儿，我写出来，请你及火车老师审查一下？

　　算了，暂不公布。相信J姐家的小五能够照着识别标准设计出秤量方案。

[ 本帖最后由 hxy007 于 2009-2-16 03:56 编辑 ].

我说老7，咱先88，明天再来验收。.

引用:

原帖由 小鹿 于 2009-2-15 22:01 发表
完全正确！  我们可是从1x2开始一项项检查才得到这个结果的！得到结果了才恍然大悟因为 16x17是17的倍数， 再加17仍然是17的倍数， 所以结果就不是质数。
后来小朋友说17这么神奇啊！  那20以内还有没有别的数 ...

　　要是在一张普通的试卷上出现这道题，我也会老老实实从1x2查起，或者倒过来从18x19查起。但要是知道是在做变态的奥数，那我可不会那么老实。我可能也会像J姐一样，首先想到的是17前后那两个数，何况17这家伙就是个质数。这种巧妙的方法好像并不是数学探究的正路，老老实实地有序试算似乎才是正门武功。

[ 本帖最后由 hxy007 于 2009-2-15 23:33 编辑 ].

哈哈，周五订了套《可怕的科学》，周日就送到了
可是多了本《太空旅行记》，少了本《电影特技魔法秀》
不过可以先看起来了.

引用:

原帖由 hxy007 于 2009-2-15 23:18 发表

　　这种巧妙的方法好像并不是数学探究的正路，老老实实地有序试算似乎才是正门武功。 ...

同意。
直觉不一定时时有，不一定事事有
在我原来的学习过程中，一直都有碰到直觉超好的同学，十分佩服，也有些崇拜。自己也偶有这种有感觉的时候，不是经常。所以，“直觉”的问题就是不太可靠，而我们学习和探究要解决的是没有直觉的时候，应该怎么办。

有且只有
就这道题而言：
4. （7分钟） 把两个小于20的连续自然数相乘， 再在积上加17.  你会发现有且只有两组自然数经过运算后结果不是质数。  找出这两组数。
作为一个命题，里边有2个关键词十分重要“找出这两组数”和“有且只有”，如果只给出的答案“16/17”和“17/18”似乎只证明了"有"，未能进一步思考“只有”。“有且只有”数学里边非常常用的表达方式，似乎数学总是已这种方式向世人证明其严密性。

没有对“只有”做进一步思考，便不会有这种感觉：
“后来小朋友说17这么神奇啊！“
也没有更进一步的探究：
”那20以内还有没有别的数也是这样的呢？  大家算了一下， 19不行（1x2+19不是质数）， 13也不行（3x4+13不是质数）。 11好像可以， 但没来得及检查到最后几组。”

后两步可能正是数学让人着迷的地方。

更正hxy007
hxy007所说“有序试算似乎才是正门武功”是不对的，应该改成“有序试算是正门武功”。

同时，我仍然会崇拜拥有直觉的人，我也会沾沾自喜于曾经拥有过的直觉。

[ 本帖最后由 ccpaging 于 2009-2-16 14:54 编辑 ].

春节期间，我带Alex及其爷爷一起拜访了我大学的老师，老师给我提出一个有针对性的建议“先立后破”，并解释到：
“立是指先教授正确的概念、理论和方法，破是指质疑概念、理论或者尝试不同的方法”
当时我仅仅是记下老师的谆谆教导，并不十分明白。

经过一段时间的思考，有一DD心得，与大家共享。

（抽空慢慢写，这似乎跟教育理论有关，请教育方面的达人多多指教）、、、

[ 本帖最后由 ccpaging 于 2009-2-16 11:58 编辑 ].

　　恭喜！祝贺！！
　　多一本少一本都没有关系。孩子能够认真读完其中的几本，就受益匪浅了。.

孩子昨晚就开始读了第一本《雨林深处》，爱不释手
与店家反映的结果是再给我一本《电影特技魔法秀》，多的《太空旅行记》也不用退了，他嫌麻烦。
谁想要我可以送一本《太空旅行记》，不过要等《电影特技魔法秀》到了才行。.

引用:

原帖由 Jupiter 于 2009-2-15 23:18 发表
我说老7，咱先88，明天再来验收。

　　JJ并火车老师等BBMM，昨天偶炮制的那个识别标准确实存在问题，表述也不清楚。已经改正过来了（见第1267楼）。根据识别标准修订版，似乎可以编制一个合乎要求的“三分重组”秤量方案。

[ 本帖最后由 hxy007 于 2009-2-16 11:45 编辑 ].

引用:

原帖由 ccpaging 于 2009-2-16 10:05 发表
hxy007所说“有序试算似乎才是正门武功。”是不对的，应该改成“有序试算才是正门武功。”

　　感谢指正！偶也是这个意思，可是，矩阵知识都丢了的人，是没有底气说得这么肯定的。.

引用:

原帖由 cks_gs 于 2009-2-16 11:42 发表

孩子昨晚就开始读了第一本《雨林深处》，爱不释手
与店家反映的结果是再给我一本《电影特技魔法秀》，多的《太空旅行记》也不用退了，他嫌麻烦。
谁想要我可以送一本《太空旅行记》，不过要 ...

我这好像多一本《电影特技魔法秀》，交换之。待我找Alex确认后，短您。

[ 本帖最后由 ccpaging 于 2009-2-16 11:51 编辑 ].

有这么巧的事？？
期待ing.

好像难度很大。而且，感觉把问题复杂化了。.

引用:

原帖由 火车是运茶的 于 2009-2-16 14:42 发表
好像难度很大。而且，感觉把问题复杂化了。

同感。似乎有一个先立再破，和如何“立”的问题。个人建议，立论如山，简单明确，尤其是全新的概念时，从最简单的入手为宜。

1、hxy007的余数研究，是一个破的过程，因为前面立的过程已在课堂教育中完成了。
2、ccpaging比较得意的集合问题，先从3个人，2：2简单问题入手，明确新的概念，以此立，再扩展到多个。
3、ccpaging比较郁闷的是爬楼梯，没有在1-4级楼梯的时候立，直接去破10级楼梯，故吃力不讨好。

一点浅见，供斟酌。

[ 本帖最后由 ccpaging 于 2009-2-16 14:51 编辑 ].

兴致勃勃跑来看答案，结果还是一头雾水，换汤不换药，吓得我也不敢讲话，现在好了，有火车开道，我说老7，全是未知的，你排来排去想干嘛？ .

还没说你呢，我好不容易来一次灵感就没你贬得一文不值！
没听说过吗，要踩着先人的肩膀往上爬，好像是这样说的如果把所有的数都验算一遍，我们就成先人了。

[ 本帖最后由 Jupiter 于 2009-2-16 14:50 编辑 ].

我崇拜有灵感的人哦！.

　　我也觉得设计上难度大，但觉得设计出来后，一看又觉得不难了。这是我的感觉，究竟如何，大家来评议。容我再检验一遍，立即上传。.