上期问题参考答案
观察风洞中飞机的固定方式,为什么用三个可变高度柱子固定飞机?柱子下面的底盘可以转动吗?为什么?
答:做个纸飞机试试。如果有三根可变长度的棍子,一个可以360度旋转的平台,我们可以得到所有的飞行姿态,平飞、爬升、俯冲等。
您认为,用算式计算和试算法计算各有什么优缺点?
答:有算式才能用算式计算。当牛顿第一次研究苹果落下的规律时,他还没有算式,只能通过不同高度落下的时间来分析归纳算式,这是试算法的一种,也几乎是他唯一可以用来寻找规律的方法。
猜猜看,在哪些情况下用算式计算更有效?在哪些情况下试算法更有效?
答:简单的算式,如计算规则形状的面积、长度、植树问题等,比较有效。没有算式,或者碰上复杂的算式时,试算法可能更有效。
试算法解题 by Alex
我在做一道题目时,遇上了麻烦,题目是这样的:
甲乙各有一个盒子,这两个盒子里的信签都是一样的。甲在每个信封里装了一张信纸,最后剩下50张信纸。乙在每个信封里装了三张信纸,最后剩下50张信封。问一个盒子里有几张信封、信纸?
(注:7月21日这天早上是忙碌的。我们来公司的路上,我给 Alex 粗略地讲了今天的安排--主要就是做这一道数学题,而且规定了他今天只能用试算法。到了公司,Alex 匆匆地记下了题目,一个人坐在他的工作位上--公司的人平时吃饭用的一张小圆桌,开始了他的试算。我则忙著做自己的工作,整个一上午都在跟同事讨论合同上的事情。期间 Alex 数次拿着他写得密密麻麻的草稿纸想问我问题,都被我打发了。一是没有时间,二是我想学习水老师的方法,打发他一个人去“生想”。)
我先用猜的方法算的。我做了一张表,可写到最后连我都不知道自己在写什么了。
(注:“生想”就像一个人孤零零地站在黑暗中,没有目标,也不知道路在哪里。他只能试着往前,实际上可能是前后左右任何一个方向,迈出一小步。可能正好踏在路上,也可能踩在烂泥里边,或者踢到一堵墙上感觉到疼痛。所以,“生想”是一种痛苦、一种折磨。正因为我体会过“生想”的可怕,不敢随随便便把 Alex 置于“生想”的境地。但想到 happyyj 妈妈说的,“纸上得来终觉浅,绝知此事要躬行”,为了得到“躬行”的诸般好处,也只好忍心这样做了。不出所料,临近中午的时候,Alex 终于还是鼓足勇气,拿着一张只写了标题的“表格”,打断了我跟同事的讨论。我们俩走到外面阳台上,在我一连串“为什么”的追问下,Alex 几乎要哭出来了。我知道,这些肯定都是他一上午百思不得其解的问题,人家就是来问这些“为什么”的,却被我抢先问了出来,自己还回答不了,超级郁闷啊。
“那么我们回到圆桌上把这个问题先慢慢地理一理吧。”我对 Alex 说:
子:好吧。
父:你先把题目比划给我看吧。
子:诺,这有一个信签盒,里边有一些信封和信签,甲在每个信封里装了一张信纸,最后剩下50张信纸。乙在每个信封里装了三张信纸、、、
父:等等,有一个信签盒还是两个信签盒?
子:好像是一个吧。
父:如果只有一个信签盒的话,甲先把里边的信封都用完了,乙就没有信封了?!
子:哦,我看看、、、应该是两个信签盒。
父:重新开始比划吧!
子:这有两个信签盒,两个盒子里的信封和信签一样多、、、
父:不对。这个话有问题。
子:哪里有问题啊?
父:题目里边没说,一个盒子里边的信封和信签一样多啊。
子:我知道你的意思,我说的是,第一个盒子里的信封和第二个盒子里的信封一样多,第一个盒子里的信签和第二个盒子里的信签一样多。
父:哦,那是你说的不对,想的是对的。看来有些话尽管啰嗦,还是不能省掉的。
子:嗯。
父:先讨论到这吧。建议你把讨论出来的规则仔细地记下来,再仔细想想。
唉、、、问题当然不是那么简单的,但我还有一份合同要改,只好再次打发 Alex “生想”去了。)
于是我写了几条规定,以后我就按照这些规定来做表格。
1) 甲乙各有一个盒子。
2) 甲乙的两个盒子里的信签都是一样的。
(注:写到纸上的时候仍然把不该省得省掉了。看来小三的文字表达和逻辑思维能力还达不到数学命题所要求的精准和清晰、、、就这样先将就着吧。)
3) 甲乙的两个盒子里的信纸至少有53张,信封51张。
下来,我就开始做了:

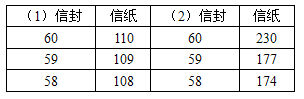
一开始,我以为我作对了,可最后我发现了,这样做的话,信纸1 和 信纸2 的差距越来越大了,而我是要它们小,所以这肯定不对。再说了,信纸我写的就不对。
(注:Alex 认真地在小圆桌上写写画画。我续水的时候经过,瞄了一眼,看到了表格,这说明 Alex 经过一上午的“生想”已经取得了不少的进展,至少他已经开始计算和填数字了,虽然填的数字不对。于是我建议 Alex 就地取材,把草稿纸裁成信封和信纸,模拟一遍题目。也许实际的模拟可以帮助 Alex 找到问题。)
我又用了一种方法,我做了许多信封和信纸,可做到最后发现数量根本就不对,更不要说计算了。
(注:已经到了午饭的时候了,Alex 把小圆桌上的草稿纸简单归置到一起。我们开始吃家里带来的午饭,一边吃一边讨论。
父:你能说说看“试算”到底是什么意思吗?
子:就是猜答案呗。
父:哦、、、今天这道题要猜什么答案呢?
子:让我看看、、、应该是猜信签盒里边有多少信封和信纸?
父:那我就瞎猜一个、、、有50张信封和50张信签?
子:那不行的,你猜的结果不符合第一个条件。
父:什么条件啊?瞎猜还要条件啊!
子:那当然啦。如果信签盒里边有50张信封和50张信签,那么甲在每个信封里边塞进一张信签,刚好把信签用完,不可能剩下50张信签。
父:哦,是这样子啊、、、那我怎么猜才能满足第一个条件呢?
子:信签少了,多加一些吧。
父:好、、、那我猜50张信封和100张信签,这样总可以了吧?
子:你猜的还是不对,不符合第二个条件!
父:还有第二个条件啊?!
子:当然啦。
父:怎么不符合第二个条件啦?
子:乙在每个信封里边塞进三张信签,还剩50个信封、、、爸爸,这个剩50个信封怎么弄啊?
父:我想想,乙在每个信封里边塞进三张信签,现在只有100张信签,一个信封塞三张信签的话、、、
子:我知道了,信签不够,就空出来许多信封。
讨论到这,我不再问了,Alex 也在默默不语地吃饭。)
最后,我尝试了一种方法,没想到竟然对了:

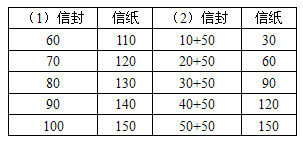
我把(1)和(2)合了起来,在做信纸时也上了心,我终于求出了答案。
(注:上午刚开始的时候,Alex 是完全摸不着方向的,他自己一个人在黑暗中挣扎,无助、混乱、沮丧。初看起来,这番挣扎并没有解决实际的问题,但其实为中午的讨论提供了非常扎实的基础。无形之中,水老师提倡的“生想”、happyyj提倡的“躬行”实实在在地提高了 Alex 探究问题的能力。)
不过,我还要进行验算呢!就用代数法吧!
信封 = A 信纸 = B
A = B - 50
B = (A - 50 ) X 3
B = 3A - 150
B + 150 = 3A
(注:Alex 知道计算的关键是消去 A 或者 B,但是他比较熟悉加减法消元(天平玩得熟),对代入法则不熟悉。我在这里干预了一次,演示了代入消元法。)
B + 150 = (B - 50) X 3
B + 150 = 3B - 150
B = 3B - 300
B + 300 = 3B
300 = 2B
B = 150
A = 100
(注:这是一个比较啰嗦的解方程步骤。不过 Alex 也才小三,不能苛求了,不忍心再苛求了、、、就这样先将就着吧。)
答:信封有100张,信纸有150张
信签题 与 “鸡兔同舞”
Alex 做完题目,脸上露出了满意的微笑,跟上午的愁云惨雾比,那是完全不同了。乘 Alex 高兴,我建议他把整个研究的过程记录下来。Alex 答应了,一个人在小圆桌上边算边些边画图。待所有的事情做完,我已经快下班了。在看 Alex 的论文时,我把题目做了一点小改动,变成这样:
甲乙各有一个盒子,这两个盒子里的信签都是一样的。甲在每个信封里装了一张信纸,最后剩下
5张信纸。乙在每个信封里装了三张信纸,最后剩下
5张信封。问一个盒子里有几张信封、信纸?
Alex 仔细看了看,算了算,带着奇怪的表情问:“这道题怎么看起来这么熟悉啊?”
父:是吗?
子:我好像做过、、、对了,我想起来了,这跟 hxy007 的鸡兔同舞是一样的啊。
父:怎么可能呢?一个是信封信签,一个是鸡兔,八竿子打不到一起啊?
子:我再想想、、、嗯,规律是一样的,绝对没错。
(编辑完毕)
[
本帖最后由 ccpaging 于 2010-7-22 17:53 编辑 ].