前天傍晚,儿子来到007身旁请教一道题:
有一项工程,12个工人需要做35天才能完成,现在要求提前5天完成,需要增加多少个工人?
(一)困境
儿子说:我觉得这道题出错了。因为35除以12,除不尽。
说的时候,他眼泪都快掉下来了。显然,儿子竭尽全力想解决问题,却没有找对路子。
007问:你为什么要用12去除35?你想干什么呢?
子:算每个人每天的做多少呀。
父:我明白了,只要知道每人每天的工作量,就能算出提前5天需要增加多少工人。
对呀,我就是这么想的。
可是,你看看题目,里边讲“12个工人需要做35天才能完成”,35除以12,得出的是每人每天的工作量吗?
嗯,不是。
当然不是。靠这道题提供的数据,我们好像算不出每人每天的工作量。
那怎么办?不知道每人每天的工作量,这道题就没有解了。
(二)假设
儿子的质疑让007想起了以前讨论过的牛顿难题。
父:题目没有说每人每天的工作量,我们可以假设呀!
子:怎么假设?我不明白。
你还记得我们去年讨论过的那个牛吃草的问题吗?当时我们也不知道一头牛一天吃多少草,我们是怎么处理这个问题的?
我们当时假定每头牛每天吃1筐草。
对,或者假定每头牛每天吃1份草。
老爸,我们这里也可以假定每个工人每天做1份事。
应该可以吧。
(三)画图作业
007嘴上同意儿子的设想,心里边对怎么解决这个问题却没有底。边做边想吧。反正是和儿子一起探讨。
父:知道了每人每天的工作量,就可以算出需要增加多少工人吗?
子:嗯,还不能,我们还必须知道总共有多少工作量。用总工作量除以30,就知道总共需要多少工人;再用这个数减去12,就可以算出需要增加多少工人。
父:你的思路很清晰。问题是,我们怎么知道总的工作量呢?
儿子立即开始计算,007赶紧制止,建议他用图画出35天里每个工人的工作量。
儿子用12根线段来表示,每根线段的1格表示一个工人一天的工作量。因为有35天,画起来很烦,儿子就用省略号表示。为了清晰起见,007现在用方格来表示。

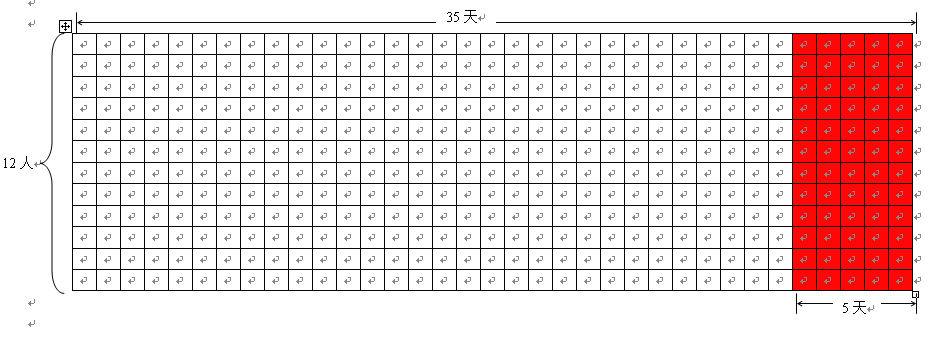
画面直观地显示了每个工人35天的工作量,实际也就显示了12个工人35天的工作量。儿子用12×35表示总工作量。
(四)解法一
父:换句话说,按照原计划,12个工人一天完成12份工作量,用了35天,总工作量是12×35。现在要提前5天完成,需要增加多少个工人呢?
儿子照着他前面说过的思路——
先求提前5天完成工程总共需要多少工人:(12×35)÷(35-5)
后求在12人基础上还需要增加多少工人:(12×35)÷(35-5)-12=2(个)
(五)解法二
儿子非常满意,急于把探索的过程和结果写在作业纸上。
007突然意识到解法不止一种:慢点,我们再看一看有没有别的解法。
有吗?
我也不知道,我们来看一看。提前5天完成,就表示原来那12个工人要少干5天,多出来的工作量就要请增加的工人来完成(见上图红色部分),对不对?
是的。
这部分工作量也必须要30天里完成,需要几个工作呢?
那要看多出多少工作量。
你算得出来吗?
1个工人多出5份工作量,12个工人就多出5×12份工作量。
那么,这些工作量在30天完成,需要几个工作来做?
5×12÷30=2,哎呀,这个解法比前面的解法更简单。
不管简单不简单,两种解法都写在作业上。第二种解法和第一种解法的结果一样,这等于是一种验证,是不是?
是的,两种方法结果都一样,我们肯定不会错了。
[
本帖最后由 hxy007 于 2010-5-21 16:25 编辑 ].