前面提到过兴趣的重要,这里说说数感的重要。
我和孩子讨论:○+△+□=17,当□=0,1,2……时,○和△分别是多少?○+△+□=17有几种情况?孩子利用他现有数学知识寻找到所有的答案(自然数范围内的所有答案),并将它们严谨而有序地排列出来。例如,当□=1时,○+△+□=17有如下可能:
0+16+1=17
1+15+1=17
2+14+1=17
3+13+1=17
4+12+1=17
5+11+1=17
6+10+1=17
7+9+1=17
8+8+1=17
9+7+1=17
10+6+1=17
11+5+1=17
12+4+1=17
13+3+1=17
14+2+1=17
15+1+1=17
16+0+1=17
在这种探讨的过程,孩子可以体会到许多数学上的东西。其中之一就是数理统计中的排列组合思想。尽管这还是一种启蒙,但孩子有了这种经历,就好像是顿悟式地领会了我后来教他的一种不漏数三角形的思路。

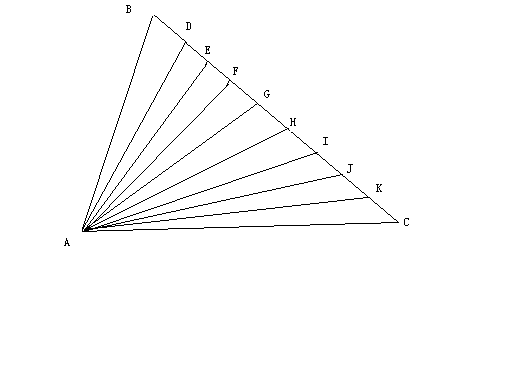
问:其中有几个三角形?
这是小学一年级学三角形时,给孩子出的一道题。孩子数得头都晕了也没有数清。我启发他:三角形就是用三条直线围成的图形,对不对?
孩子点头。
直线AB可以和BD、AD围成一个三角形ABD,对不对?
对。
直线AB还可以和哪些直线围成三角形?
孩子按照顺序一个一个数出来了:三角形ABE、ABF、ABG、ABH、ABI、ABJ、ABK、ABC,加上ABD一共9个。
那么,用同样的方法,数一下AD可以和别的线条可以组成几个三角形?
可以组成三角形ABD、ADE、ADF……,总共也是9个。
ABD这个三角形前面算过,这里不能算了。那么,还有几个?
8个。
再用前面的方法数一下:AE可以和别的线条组成几个三角形?注意,数过的不要数了。
孩子一数:有7个。他突然大声道:不要数了,我知道后面还有几个三角形。第一条线可以组成9个,第二条线可以组成8个,第三条线可以组成7个,后面肯定是6个、5个、4个、3个、2个、1个。
对,你的想法是对头。那么,总共有几个?
孩子列出一个连加的算式:9+8+7+6+5+4+3+2+1=
孩子正要用平常的方法计算,我问:有没有更聪明的方法计算?
孩子想了一下,说:9加1等于10,8加2等于10,7加3等于10,6加4等于10,还剩下一个5,总共是45.总共有45个三角形。
对!这是一种聪明的算法。
我问:数学是不是很有意思?
儿曰:太有意思了!
我说:再来!假定在原来的图中再加一条线AL,那么,总共有几个三角形?
孩子快速地列出了算式:10+9+8+7+6+5+4+3+2+1=
好,我们再用前面的聪明方法,10加1,9加2……看看:有几个11?
没有想到的是,孩子说:爸爸,你笨了!这种方法一点都不聪明。前面我刚刚算出9+8+7+6+5+4+3+2+1=45,现在加上一个10,不就是55吗?总共有55个三角形。
是我笨,但我由衷地为孩子感到欣慰。当时,我几乎被孩子的灵活与聪明劲给雷倒。
晚上,孩子把这个题目出给他妈妈做。孩子他妈数得七荤八素,最后也没有数出来。孩子在一旁“幸灾乐祸”,看着妈妈出尽洋相,几乎笑爆。当孩子像个老师一样教他妈妈怎样统计时,我在一旁遐想:孩子总是这样学数学,该是一件多美的事!
孩子从中领略到的并不仅仅是数学的趣味,还有一样难得是数学的思想——严谨而有序的排列组合思想。这种思想和方法在前面就有启蒙,在这里得以深化,并且迁移到了后面的学习中。接下来,老师布置作业——数长方形,孩子已经能够自己独立解决问题了。

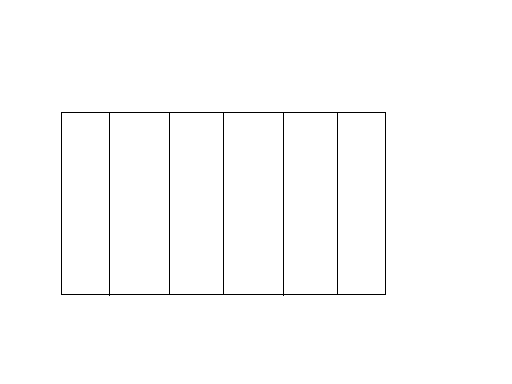
让孩子数这里面有几个四边形,小菜一碟!6+5+4+3+2+1=21
让孩子学到这种数学思维,需要时间、耐心,让孩子慢慢来。可是,这个功利而浮躁的世界不容许我们的孩子慢慢来。学得虽快,却不扎实。做题正确,却得不到数学的精义。
[
本帖最后由 hxy007 于 2008-12-18 08:33 编辑 ].